Home
Research
Overview Publications and Software Selected Talks
Teaching
Overview UWM Teaching Duties TAMU Teaching Duties
Projects
Real Geometry in M2 Cox Homotopies in julia Decomposable Systems in M2

Profile

Overview

I'm a Van Vleck Visiting Assistant Professor at University of Wisconsin - Madison with expertise in applied and computational algebraic geometry and their applications to machine learning and statistics. I have a passion for excellence in meeting my team's goals by developing creative and original solutions to problems, and effectively communicating those solutions.

Image not found!
Resume
Image not found!
CV

Education

Organizational Work

Research

Overview

My research focus lies in numerical and computational algebraic geometry and their applications to areas such as to machine learning and statistics. More specifically, some of my mathematical interests include, in no particular order:

Much of my research is accompanied by technical open-source software which is freely available to use and is hosted on my Github and/or official sources as provided in Publications and Software below. These software implementations vary widely in the scope of their audience and application, from black-box solvers for general polynomial systems to more technical software for the purpose of research experimentation and proof. See Projects below for details on selected examples.

Publications and Software

Preprints (reverse-chronological):

Publications and Software (reverse-chronological):

Selected Conference/Seminar Talks

Teaching

Overview

My teaching philosophy is that students prosper in an environment that allows them to confidently learn and apply mathematics, without fear of failure or ridicule. In my various roles as mathematics tutor, TA, and instructor, I've taught a wide range of topics from lower-level undergraduate courses through graduate level topics courses. In each of these settings, I've found success by actively engaging with students and allowing them to explore and understand the material in their own way. Several past students have voiced their appreciation for my style of teaching through course evaluations and by reaching out personally. Classroom evaluations from students are available on request from appropriate parties, below are selected comments from these evaluations:

As a direct result of my approach to teaching, I've been awarded the Postdoctoral Excellence in Teaching Award from the Department of Mathematics at University of Wisconsin - Madison and the Outstanding TA Award from Texas A&M University.

University of Wisconsin - Madison Teaching Duties

Texas A&M University Teaching Duties

Texas A&M University Teaching Assistant Duties

Selected Projects

Real Geometry in Macaulay2

This project led to the development of the RealRoots.m2 Macaulay2 package. This package implements several symbolic methods from real algebraic geometry including:

This work also resulted in an improved statement and proof of Sylvester's theorem, which allows one to compute information about the real zeros of a polynomial system more accurately. The article "Real Solutions to Systems of Polynomial Equations in Macaulay2" provides a complete description of the implemented methods and mathematical content.

We illustrate the utility of this package via an example. It is well known that a smooth cubic surface in complex projective 3-space contains 27 distinct lines, that lie entirely on the surface. However, a smooth cubic surfaces in real projective 3-space can contain only 3, 7, 15, or 27 lines. By describing these lines as solutions of a polynomial system, the RealRoots.m2 package can be used to determine this number of lines for a given cubic surface.

The illustration below is of the cubic surface defined by the equation

58313/630 x3 + 13351/1260 x2y - 2645/84 xy2 + 1997/180 y3 + 1869/20 x2z + 769/105 xyz - 323/90 y2z - 27/20 xz2 - 4751/90 yz2 + 12053/630 z3 + 1073/120 x2 - 883/120 xy - 977/252 y2 - 8737/504 xz + 2171/360 yz + 541/8 z2 + 1079/210 x - 30977/1260 y - 36767/630 z - 6953/1260 = 0.

At a glance, it is unclear how many lies lie on this cubic surface. Using RealRoots.m2, it can be proven that the cubic surface below contains the maximum number, 27 lines. These lines are illustrated on the surface below in red. Please click on the figure below for an interactive view of the surface and all 27 lines.

Image not found!
Figure 1: A smooth cubic surface containing 27 distinct lines. Interactive viewer.

Cox Homotopies in julia

The julia software package CoxHomotopies.jl implements numerical homotopy algorithms described in the research article "Polyhedral Homotopies in Cox Coordinates". We briefly describe numerical homotopy algorithms in general, and the methods contained in this software package.

A numerical homotopy algorithm utilizes a start system whose solutions are known or easier to compute to compute solutions of other systems. To compute solutions of a given target system, F, a homotopy is constructed, which can be considered as a path between the start system G and the target system F. A numerical homotopy algorithm tracks the solutions of the start system along the homotopy, to obtain solutions of the target system. In the illustration below, the start system G has 3 solutions that get tracked to 2 solutions of the system F.

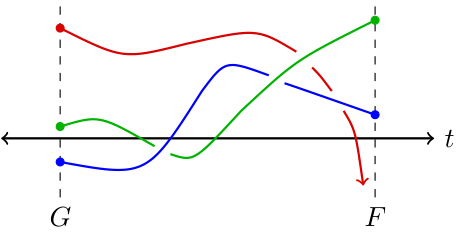
Image not found!
Figure 2: An illustration of a homotopy between a start system G and a target system F.

Note that in the illustration above, the red curve seems to diverge--it does not provide a solution to the target system F. Alternatively, the red curve could end at a solution of the target system F which is very large in magnitude. In either case, accurately tracking along the red path is computationally expensive and potentially leads to inaccurate or unnecessary information.

The main method of CoxHomotopies.jl provides a numerical homotopy algorithm for solving polynomial systems. Loosely, this algorithm ensures no paths diverge as in the illustration above. This is achieved through a toric compactification of the solution space--solutions are tracked in a quasi-affine space which provides coordinates for the toric compactification via the Cox quotient construction of a complete normal toric variety.

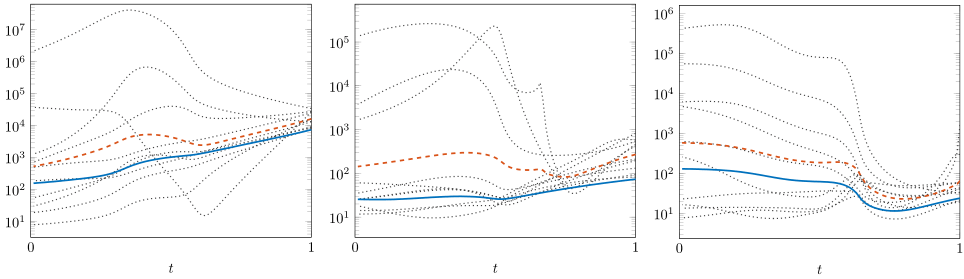
Image not found!
Figure 3: The graphs above illustrate the condition number of the Jacobian matrix during the tracking of 3 solutions in a particular numerical experiment. In each graph, the dotted lines represent a random choice of hyperparameters, the dashed red line represents the average condition number for these random choices, and the blue line represents the achieved condition number through the use of the Cox homotopy algorithm.

This algorithm has the additional benefit that extra hyperparameters are introduced during tracking. Numerical experiments detailed in "Polyhedral Homotopies in Cox Coordinates" illustrate that these parameters may be chosen in a consistent way as to decrease the condition number of the Jacobian of the system while tracking. This is expressed by the figures above.

Solving Decomposable Systems in Macaulay2

The Macaulay2 package DecomposableSparseSystems.m2 implements methods of decomposing sparse polynomial systems into simpler systems. The article "Decomposable Sparse Polynomial Systems" details the methods contained in this package, and the Journal of Software for Algebra and Geometry has peer-reviewed the code and documentation in addition to this article.

Whether or not a sparse polynomial system decomposes can be determined by its Galois group, as described in the research article "Solving Decomposable Sparse Systems". While the Galois group may be difficult to determine, theoretical tools for understanding the Galois group provide a classification of those systems which decompose. Those sparse polynomial systems that decompose are those lacunary systems and triangular systems.

The main method of DecomposableSparseSystems.m2 iteratively decomposes systems until no further decomposition is possible. This is provided as overhead for a black-box solver, which solves the resulting decomposed systems, and the method recombines solutions into solutions of the original system. The figure below shows the results of a computational experiment comparing the timing of using the black-box solver PHCPack agains the main method of DecomposableSparseSystems.m2, in the precense of decomposable systems.

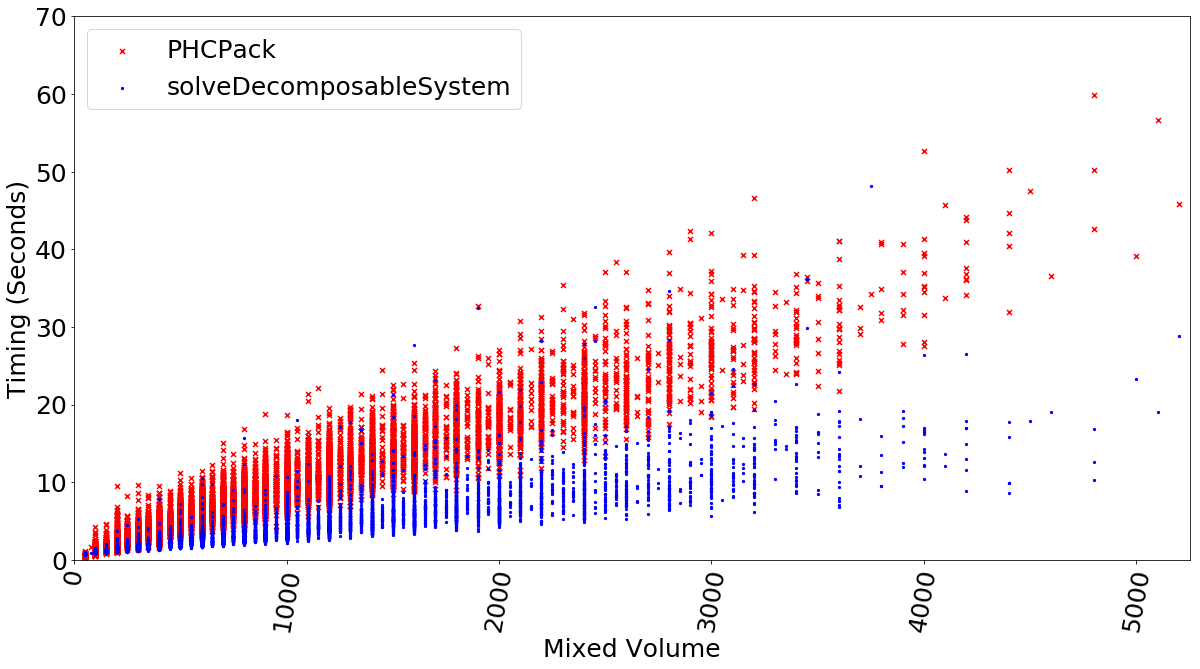
Image not found!
Figure 4: The timings of PHCPack and DecomposableSparseSystems.m2 in solving over 10,000 instances of decomposable sparse polynomial systems with up to 5,000 solutions.